Tree

樹的概念

樹是一種重要的離散結構(discrete structure)，提供「具有層次關係」的概念來結構資料。生活中常見的樹有「族譜」、「演化樹」、「組織架構」、「運算樹」等等。

專有名詞

定義

樹為節點組成的有限集合，其中

(1) 存在一特殊節點R稱為樹根(root)

(2) 其他節點可分成n個無交集的集合:T1,T2,...,Tn，n≧=0，而T1,T2,...,Tn 本身皆為樹，稱其為R的子樹(subtree)

在定義中，各子樹T1,T2,...,Tn亦沿用了樹的定義(遞迴)。

圖1描繪了一棵「有根樹」(rooted tree)，並搭配下列名詞簡介(下文若無特別強調皆為此類樹)；圖2為「無根樹」(unrooted tree)，常在不需考量節點間資料關係時使用(亦即無階層概念)。

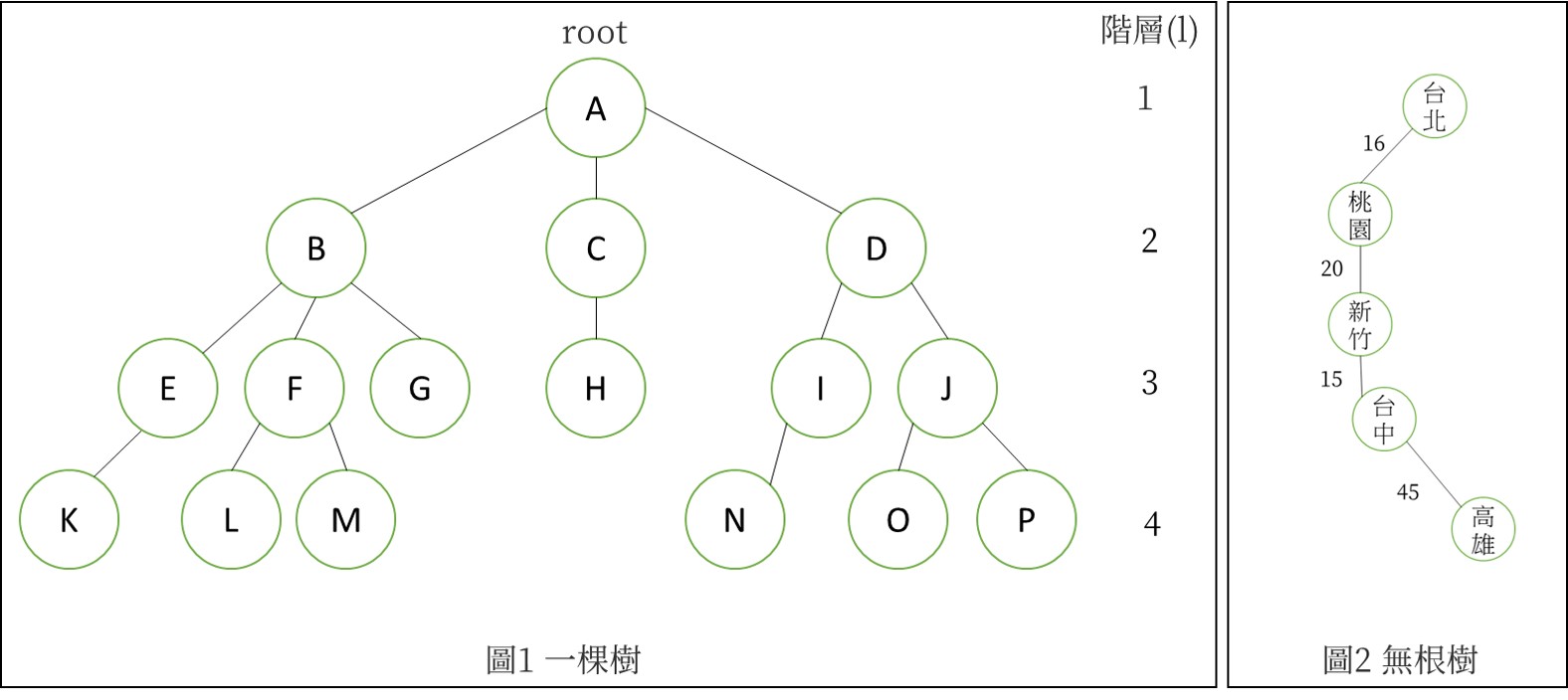
• node 節點: 圓圈所標明之資料及向下分支的合稱。共16個。
• root根 : node A 。
• degree分支度 : 一個node的所有子樹的數目。例如A的degree為3、C為1，D為2。一棵樹的degree為其所有node中degree最大者，圖1即為3。
• leaf (or terminal node ) : degree為0的node(即其無任何子樹)，如GHKLMNOP。
• non-terminal node : 任何非termianl node。
• child (son) : 任何節點之子樹的樹根。BCD皆為A的son。
• father(parent) : A為BCD的father。
• sibling(brother) : 共有一個father之node。例如BCD、EFG。
• ancestor : 任一節點走向樹根所經過的所有節點。例如L的ancestor為FBA。
• descendant : 任一節點的所有子樹節點。例如D的descendant為IJNOP。
• level(l) : 定義階層l枝節點其son的階層為l+1。
• depth(height) : 樹的最高階層。圖1為4。

樹的表示方法

陣列可表示樹，然而會較為困難。此以鏈結串列(linked list)表示，假設一棵樹T的分支度為K，即T中存在節點X其分支度為k，為使鏈結節點可存放X點的k個子數指標。每個節點須有k個指標的記憶體位置，若此樹有n個節點則需要nk個指標位置。然而除了root以外，每個節點僅需一個指標指向，亦即只需n-1個指標位置，因此多用的空間為nk-(n-1)=n(k-1)+1，非常浪費空間。於是介紹下列三種表示方法:一般化串列、左子右兄弟、分支度為2的表示法。

一般化串列表示法(gernalized list)

之前學到的串列可用A=(a1,a2,...,an)表示，為有限且有序之集合；每元素ai，1≦i≦n，皆有相同資料型態。若不限定須有相同資料型態則稱為一般化串列(gernalized list)，於是a可以是node也可以是tree，因此用其來表示一棵樹T :

T = (R,T1,T2, ... ,Tn)

T1,T2, ... ,Tn為R的子樹，Ti可能為節點或樹(遞迴)。

範例

圖1的一棵樹可表示成一般串列如下:

T = (A,(B,(E,K),(F,L,M),G),(C,H),(D,(I,N),(J,O,P)))

若將節點A的三個兒子BCD所形成之子樹，分別取名為T1,T2,T3則可簡化為

T=(A,T1,T2,T3) ，其中

T1 = (B,(E,K),(F,L,M),G)

T2 = (C,H)

T3 = (D,(I,N),(J,O,P))

如圖3串列中的元素可能是某一樹上的節點或一子樹；而圖4鏈結節點中的欄位也有可能是樹節點資料R，也可能是子樹Ti(1<=i<=n)的指標，因此可新增一個節點欄位tag來區別。在C語言中可用union來達成節點宣告。

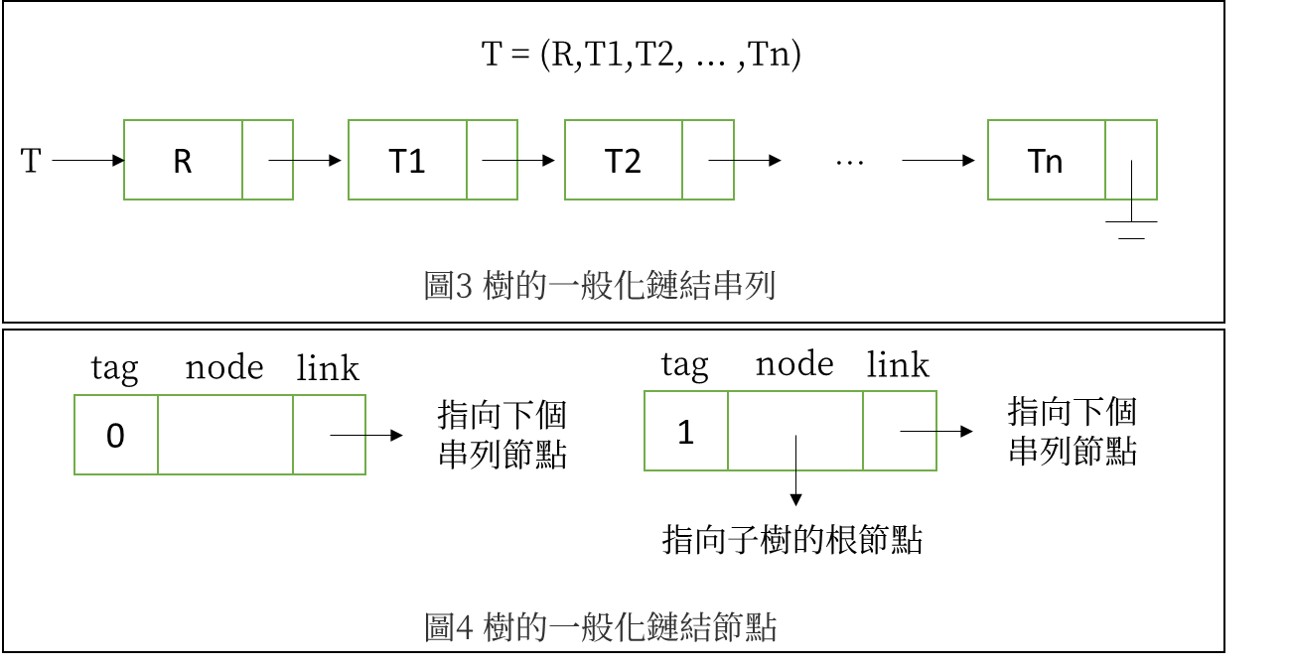
union節點宣告

struct TreeNode
{
    int tag;//用tag區分,欄位node的資料型態
    //union:編譯器在編譯階段會預留空間(int or  struct TreeNode指標中較大者))
    union
    {
        int data;
        struct TreeNode *Tlink;
    }node;
    struct TreeNode *link;
}

實作結果示意圖

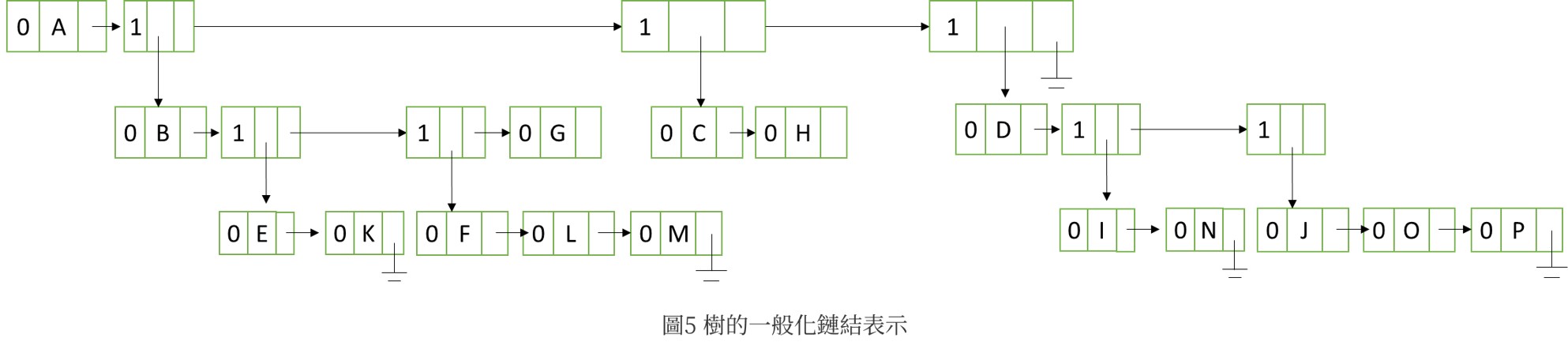
左子右兄弟表示法

觀察圖1的樹，可以發現每個節點都有唯一的 最左兒子(leftmost child)；也有一個最靠近它的右兄弟(rightmost sibling)，圖1可轉換成圖6，每個節點結構為圖7；，鏈節串列如圖8。

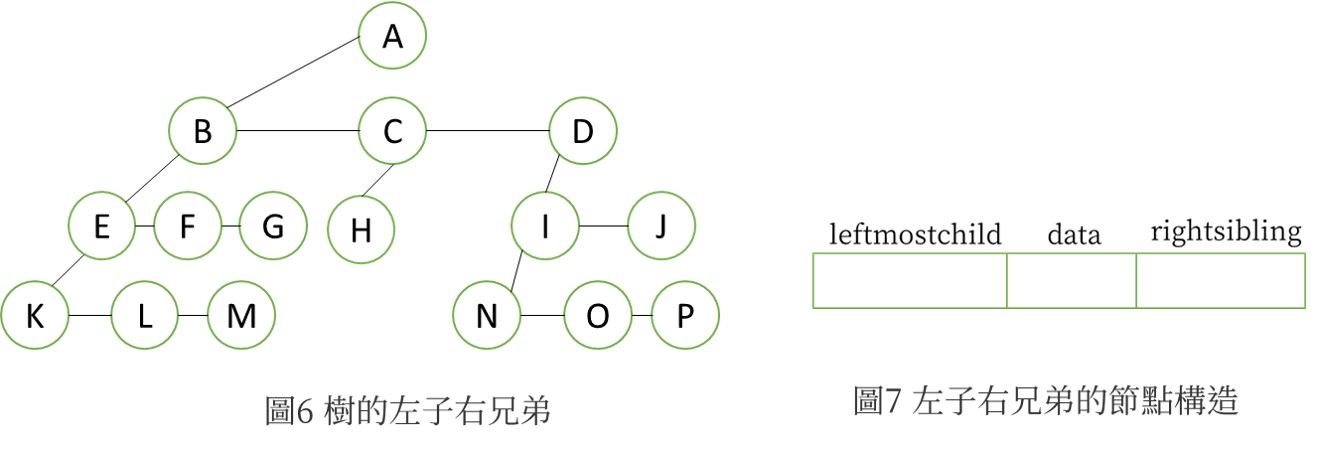
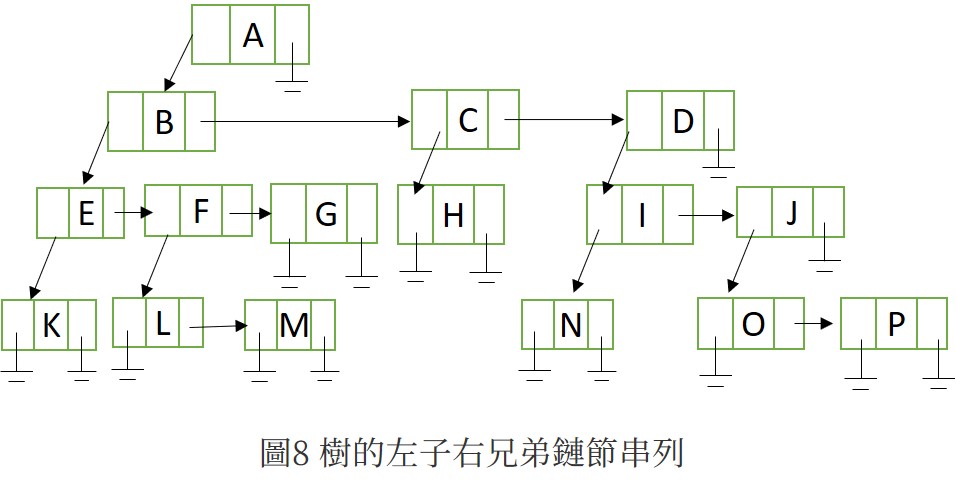
分支度為2的表示法

將左子右兄弟稍微旋轉可以得到degree為2的樹，稱為二元樹(binary tree)(圖9)。二元數可以用來表示任何樹!

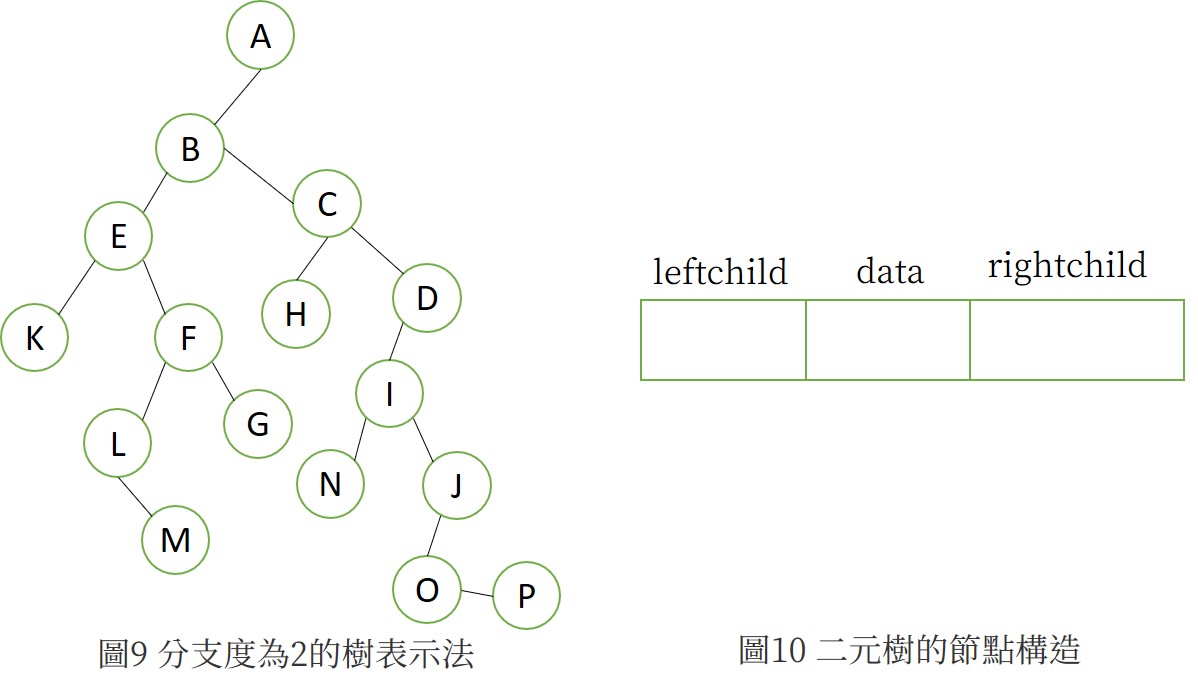
二元樹

二元樹結構簡單且容易表示(可用陣列或鏈結串列表示)，更有許多有用的性質，且任何樹皆可用此表示!因此是一項非常重要的資料結構。任一節點最多有兩分支且有左右之分。

定義

二元樹是一個由節點組成的有限集合，可以是空集合，或是包含了

(1) 一個樹根節點；

(2) 其他節點分割成兩個沒有交集的二元樹 : 一為左子樹(left subtree)；一為右子樹(right subtree)。

樹與二元樹間的差異:

1. 樹不可有空節點，而二元樹可以。
2. 樹的子樹沒有順序，而二元數的子樹有左右之分。

範例

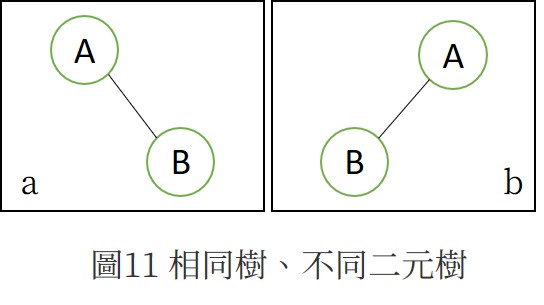
樹和二元樹的共同基本性質

定理 1: 若一棵樹T的總節點樹為V，總邊樹為E，則 V=E+1。

二元樹的性質

二元數可容納的節點樹與深度似乎有極大關係。圖12的特殊例子表示兩種樹 - 完備二元樹(complete binary tree) 及 歪斜樹(skew tree) ，兩者具有同樣的節點數，然而歪斜數需要較多階層來存放。

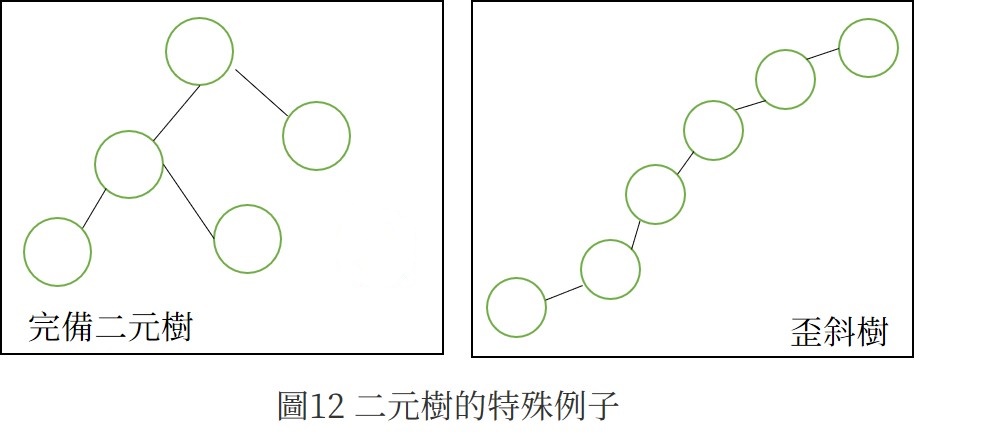
定理 1 :

(1) 二元樹上階層i的節點數目最多為2^(i-1)，i≦1;

(2) 深度為k的二元樹，其節點數目最多為2^k -1，k≧1。

定理 2 :

若T為一非空的二元樹，n0為樹葉節點數目，n2為分支度為2的節點數目，則n0=n2+1。

完滿二元樹(full binary tree)

定義 : 一個深度為k的完滿二元樹即為一深度為k且有2^k -1個節點的二元樹，k≧0。

完備二元樹(complete binary tree)

定義 : 深度為k，節點數為n的二元樹為完備二元樹，若且唯若 :

(1) k=1時，樹有一個節點；

(2) 當k≧2且1≦ i < k時，深度 i 有 2^(i-1) 個節點，且第k層的節點皆由第k-1層的分支由左至右逐一連接而成。

By定義，缺口一定在右下角。

由定理1可得

n 個節點的完備或完滿二元樹，其深度為[log2(n+1)] (高斯取頂符號打不出來@@)

正規二元樹(formal binary tree)

常用於單淘汰賽制，由定理2 : n0=n2+1，可推導出單淘汰賽制中自n個隊伍中產生冠軍須舉辦n-1場比賽。

定義 : 若二元樹中internal node內部節點(亦即所有非樹葉的節點)恰有兩個子節點。

二元樹表示法

用陣列表示樹很不方便，而二元樹結構較單純，可用陣列來表示。以下將以陣列及鏈節串列兩種方式表示二元樹。

陣列表示二元樹

定理1 : 若有一個具有n個節點的完備二元樹以循序的方式編號，並依序存放在陣列A中，即第i個節點存放在A[i]中，1≦i≦n，則

(1) 節點i的父親節點位在A[i/2]中，i≠1(i=1時，其節點正為樹根，無父節點)。

(2) 若2i≦n，節點i的左兒子節點位在A[2i]處；若2i>n，節點i沒有左兒子節點。

(3) 若2i+1≦n，節點i的右兒子節點位在A[2i+1]處；2i+1>n，節點i沒有右兒子節點。

依上述定理，將圖12的樹存放在陣列中如圖13，可以發現歪斜樹會浪費空間及時間，深度為k的二元樹擁有2^k -1個可放節點的空間，若存放深度k的歪斜樹只用到k個空間!

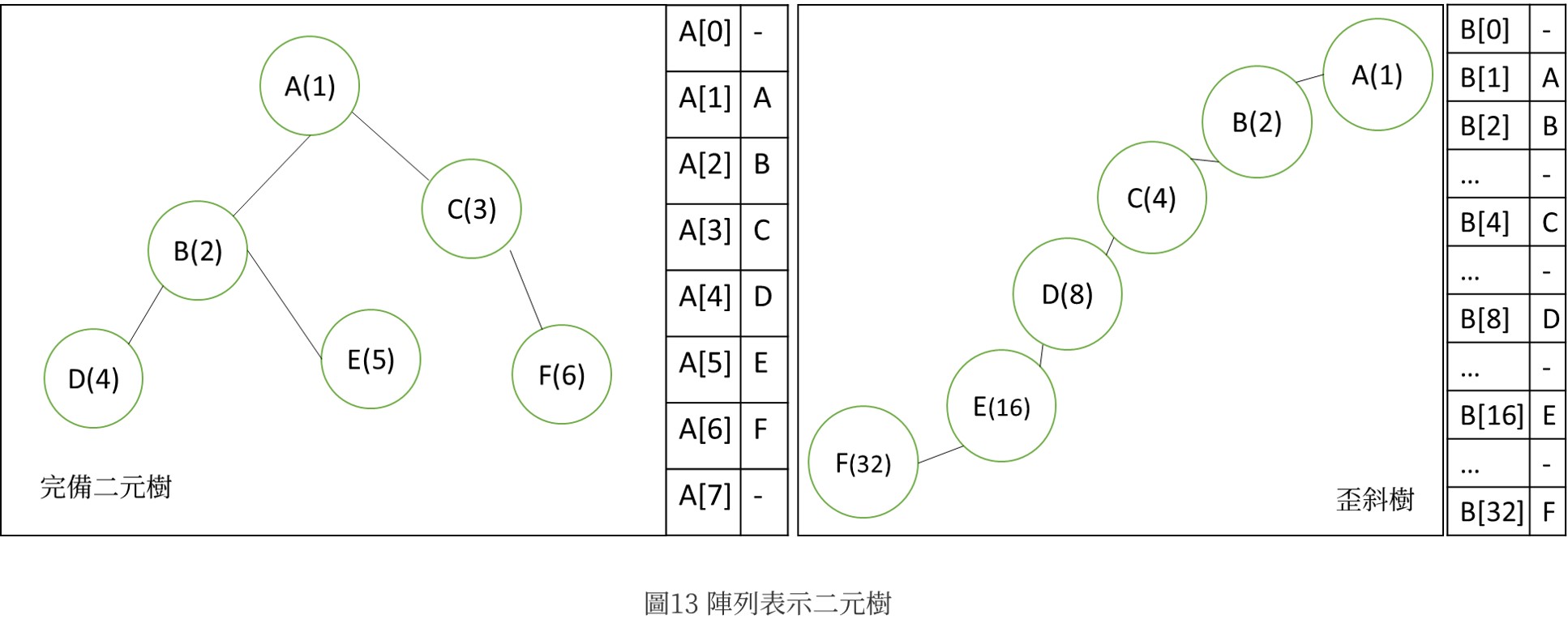
鏈節串列表示二元樹

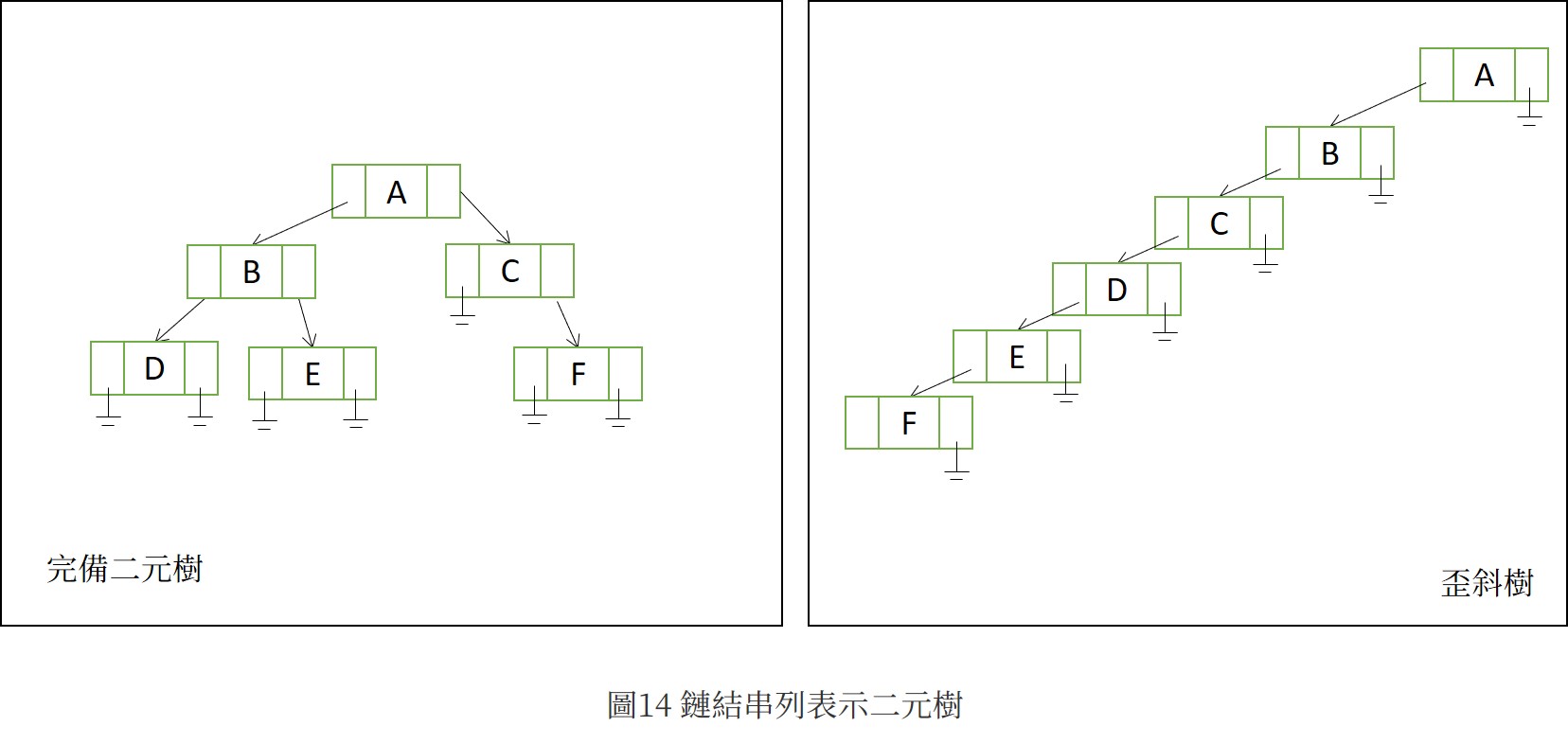
陣列表示完備二元樹以相當方便，但是使用陣列時如果資料需要頻繁的新增刪除則會非常耗時，因此可嘗試以鏈結串列表示(圖14)。可用一指標root指向樹根，作為樹鏈節串列的起點。圖13和14比較可以發現完備二元樹在兩種方法都較不會浪費空間；而歪斜樹的陣列表示法可能需要2^n -1個陣列元素，串列僅需n個，所以有2^n -1-n的空間被浪費。

圖14的節點結構在取得兒子節點的指標很方便，但是父節點的取得則無法滿足，因此可依需求自行定義鏈結節點，加上一欄位指向父節點。此外，可以發現樹葉向下指的兩個指標皆會指向NULL，這項特性引發了引線二元樹的靈感(下面會提到)。

二元樹走訪

對全資料做動作例如:計算所有數目、印出所有資料、在所有資料中搜尋某項資料...等時，即需要對二元樹進行走訪(traversal)運算，再走訪的同時進行計算列印或搜尋等動作，希望發展的走訪演算法可以對每一節點皆一致，方便撰寫程式實作。

以圖15為例，若對一樹節點而言，V代表處理節點資料，L代表走訪其左子樹，R代表走訪其右子樹，共有六種走訪組合，又因對稱的緣故，可以只考慮左子樹一定會先於右子樹被走訪，因此剩下三種順序，以V對應位置取名。

節點結構宣告

struct BTreeNode
{
  struct BTreeNode *leftchild;
  char data;
  struct BTreeNode *rightchild;  
};
struct BTreeNode *root;

圖16為運算是利用三種方式走訪之結果，可以發現就是利用遞迴的方式，事實上，二元樹的建構也是建立在遞迴觀念之上。

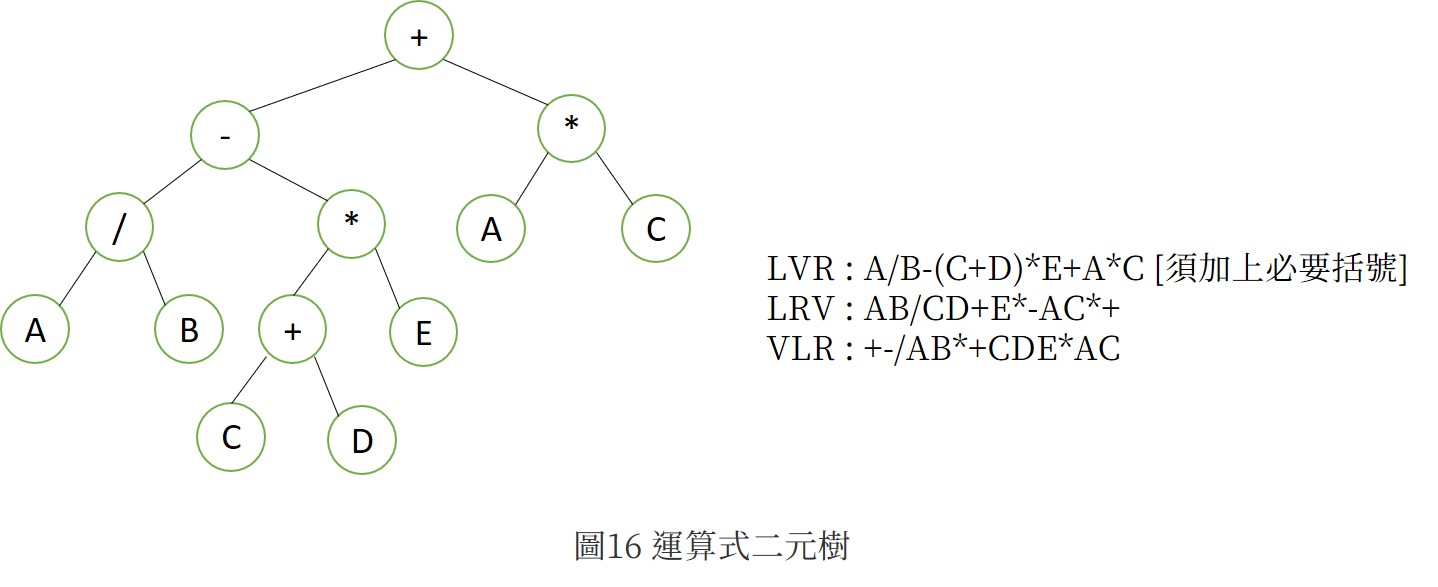
中序走訪LVR

void inoreder(struct BTreeNode *node)
{
    if(node!=NULL)
    {
        inorder(node->leftchild);
        cout<<node->data;
        inorder(node->rightchild);
    }
}

後序走訪LRV

void postoreder(struct BTreeNode *node)
{
    if(node!=NULL)
    {
        postoreder(node->leftchild);
        postoreder(node->rightchild);
        cout<<node->data;
    }
}

前序走訪VLR

void preorder(struct BTreeNode *node)
{
    if(node!=NULL)
    {
        cout<<node->data;
        preorder(node->leftchild);
        preorder(node->rightchild);
    }
}

藉由以上程式碼，基本上要得到走訪結果僅需呼叫inorder(root);、preorder(root);、postorder(root);需注意的是中序走訪還須加上必要的括號，以得到正確運算式。

利用堆疊和迴圈方式實作

中序走訪LVR

//宣告節點構造
struct BTreeNode
{
  struct BTreeNode *leftchild;
  char data;
  struct BTreeNode *rightchild; 
};
struct BTreeNode *root;//指向樹根
//宣告堆疊元素結構
struct stackNode
{
    struct BTreeNode *treenode;
    struct stackNode *next;
};
struct StackNode *top;//指向堆疊頂端
//push
void push_StackNode(BTreeNode *node)
{
    struct stackNode *oldtop;//新指標存舊的top
    oldtop = top;
    top = (struct stackNode*)malloc(sizeof(struct stackNode));//分配空間給新節點
    top->treenode = node;
    top->next = oldtop;//新節點連向舊節點
}
struct BTreeNode *pop_StackNode()
{
    if(top==NULL)//stack is empty
    {
        StackIsEmpty();
    }
    else
    {
        struct stackNode *node;
        struct stackNode *oldtop;
        oldtop = top;
        node = top->treenode;
        top = top->next;
        free(oldtop);
        return node;
    }
}
void inorder_Stack(struct BTreeNode *node)
{   do
    {
        while(node!=NULL)
        {
            push_StackNode(node);
            node = node->leftchild;
        }//push all leftchild
        if(top!=NULL)
        {
            node = pop_StackNode();
            cout<<node->data;
            node = node->rightchild;
        }//print data and check rightchild
    } while(top!=NULL || node!=NULL);
}

前序走訪VLR

中序和前序的差異僅在:輸出V的時機，中序遇到V時先放入堆疊去找左子節點；前序則直接印出。所以可以用中序的概念去修改實作出。

void preorder_Stack(struct BTreeNode *node)
{   do
    {
        while(node!=NULL)
        {   cout<<node->data;
            push_StackNode(node);
            node = node->leftchild;
        }//push all leftchild
        if(top!=NULL)
        {
            node = pop_StackNode();
            node = node->rightchild;
        }//print data and check rightchild
    } while(top!=NULL || node!=NULL);
}

後序走訪LRV

LRV反轉後即為VRL，反之亦然，因此可以先求出VRL結果再進行反轉。好處在於VRL可以用上面取得前序(VLR)的方法來實作，我們多宣告push_data(node)、pop_data()、top_data來實作。

struct StackNode *top_data;
void push_data(struct BTreeNode *node)
{
    struct StackNode *oldtop_data;
    oldtop_data = top_data;
    top_data = (struct stackNode*)malloc(sizeof(struct stackNode));
    top_data->data = node;
    top_data->next = oldtop_data;
}
struct StackNode *pop_data()
{
    if(top_data==NULL)
    {
        StackisEmpty();
    }
    else
    {
        struct BTreeNode *node;
        struct StackNode *oldtop_data;
        oldtop_data = top_data;
        node = top_data->data;
        top_data=top_data->next;
        free(oldtop_data);
        return node;
    }
}
void postorder_Stack(struct BTreeNode *node)
{   do
    {
        while(node!=NULL)
        {   push_data(node);
            push_StackNode(node);
            node = node->rightchild;
        }//push all leftchild
        if(top!=NULL)
        {
            node = pop_StackNode();
            node = node->leftchild;
        }//print data and check rightchild
    } while(top!=NULL || node!=NULL);
    while(top_data!=NULL) cout<<pop_data();
}

階層走訪(level-order traversal)

走訪階層由小至大，同一階層則從左至右。對同一階層而言，先走訪的節點，其子節點也會在下一階層先被走訪，有FIFO的特性，用佇列queue來實做。

//宣告節點構造
struct BTreeNode
{
  struct BTreeNode *leftchild;
  char data;
  struct BTreeNode *rightchild; 
};
struct BTreeNode *root;//指向樹根

struct Qnode
{
    struct BTreeNode *BTnode;//指向資料(為BTreeNode)
    struct Qnode *next;//指向下一個Qnode
};
struct Qnode *front;
struct Qnode *rear;
void AddQueue(struct BTreeNode *Tnode)
{
    struct Qnode *node;
    node = (struct Qnode *)malloc(sizeof(struct Qnode));
    node->BTnode = Tnode;
    node->next = NULL;
    if(front==NULL)//new Queue
    {
        front = node;
    }
    else
    {
        rear->next = node;
    }
    rear = node;
}
struct BTreeNode *DeleteQueue()
{   struct BTreeNode *node;
    struct Qnode *oldfront;//存要被刪除元素的指標作為free用
    if(rear==NULL)
    {
        QisEmpty();
    }
    else
    {
        oldfront = front;
        node = front->BTNode;
        front = front->next;//front往下指
        free(oldfront);
        return node;
    }
}
void LevelOrder(struct BTreeNode *node)
{
    AddQueue(node);
    while(front!=NULL)
    {
        node = DeleteQueue();
        cout<<node->BTnode;
        if(node->leftchild!=NULL) AddQueue(node->leftchild);//依序走訪左右
        if(node->rightchild!=NULL) AddQueue(node->rightchild);
    }
}

二元搜尋樹(binary search tree)

定義

二元搜尋樹是一棵二元樹，可能是空二元樹，若不為空二元樹，則滿足下列性質:

(1) 所有節點內的資料性質是相異的 *(非必要，在此方便討論)。

(2) 左子節點的資料內容(如果有) 要比父子節點的資料內容小。*(和1有關)

(3) 右子節點的資料內容(如果有) 要比父子節點的資料內容大。*(和1有關)

(4) 以左和右子節點為樹根的左子樹和右子樹也是二元搜尋樹。(遞迴概念)

依照定義，圖17中ab皆為二元搜尋樹，C則不。

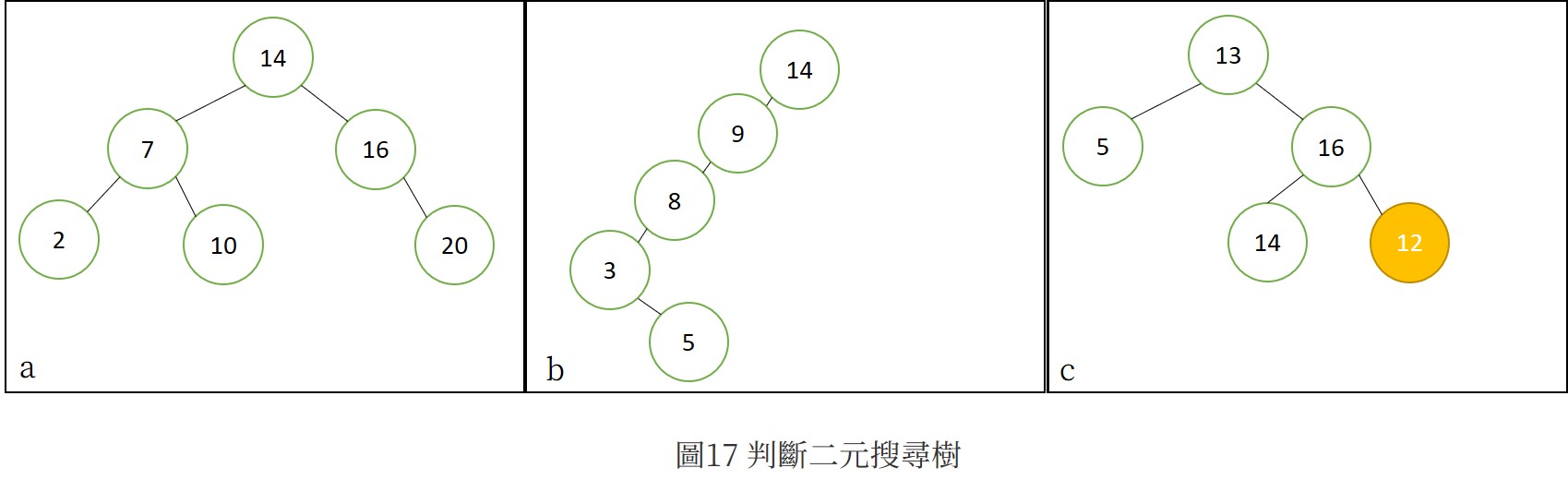
搜尋資料

利用二元搜尋樹對資料大小排序非常明確的特質，可以在搜尋資料時更為方便，以下以遞迴及非遞迴的方式撰寫。非遞迴的方式會較有效率!若有保留走訪資訊的需求可以加入堆疊儲存資料。

計算時間複雜度時，考量最差情況為「愈搜尋資料根本不在樹裡」，因此為O(h)，h為樹高，若樹有共n個節點，則logn≦h≦n。由此可知樹的高度會影響搜尋速度，因此有學者提出「高度平衡樹」(AVL tree)，將樹的高度控制在logn，即可將時間控制在O(logn)，是非常重要的做法。

(以下二元搜尋樹定義為右子節點≧父節點、左子節點＜父節點。)

遞迴搜尋

//declaration node
struct BSTreeNode
{
    struct BSTreeNode *leftchild;
    int data;
    struct BSTreeNode *rightchild;
};
struct BSTreeNode *root;//point to root
struct BSTreeNode *SearchBST(struct BSTreeNode *tree,int x)
{
    if(tree==NULL) return NULL;//not found
    if(tree->data==x) return tree;//found
    if(tree->data<x) return SearchBST(tree->leftchild, x);//find at leftside
    return SearchBST(tree->rightchild, x);//otherwise find at rightside
}

非遞迴搜尋

struct BSTreeNode *SearchBST_interative(struct BSTreeNode *node,int x)
{
    while(node!=NULL)//if still have somewhere not searched,keep searching.
    {
        if(node->data==x) return node;
        if(node->data<x) node = node->leftchild;
        else node = node->rightchild;
    }return NULL;
}

新增資料

插入資料進二元搜尋樹時，為維持資料大小關係，必須知道可以插入的位置!由於先前限定資料必相異，因此在插入資料時，可以先進行搜索，當搜尋結果為NULL時即為該插入的位置。因此，資料結構老師的名言:

徐子曰 : 搜尋未果處，新增其也。

遞迴

在程式中利用不斷搜尋遞迴呼叫，當節點被插入時會一層層的回傳直到根節點，讓節點的父親都能知道新增了一代!

struct BSTreeNode *NewBSTNode(int x)
{
    struct BSTreeNode *node = (struct BSTreeNode *) malloc(sizeof(struct BSTreeNode));
    node->data = x;
    node->leftchild = NULL;
    node->rightchild = NULL;
    return node;
}
struct BSTreeNode *InsertBSTnode(struct BSTreeNode *node,int x)
{
    if(node==NULL) return NewBSTNode(x);//搜尋未果處，新增其也
    if(x<node->data)//go left
        node->leftchild = InsertBSTNode(node->leftchild,x);
    else
        node->rightchild = InsertBSTNode(node->leftchild,x);
    return node;
}

非遞迴

「搜尋未果處，新增其也」的概念依舊沒變，然而父子的關係就必須手動進行維護!

void BSTreeNode *InsertBSTnode_iterative(int x)
{
    struct BSTreeNode *father,*son;
    son = root;father=NULL;//init ；root is global variable
    while(son!=NULL)
    {
        father = son;//記住父節點後，往下搜尋
        if(x<son->data) son = son->leftchild;
        else son = son->rightchild;
    }
    //當node son ==NULL時，搜尋未果處，新增其也
    son = (struct BSTreeNode *) malloc(sizeof(struct BSTreeNode));
    son->data = x;
    son->leftchild =NULL; 
    son->rightchild =NULL;
    if(root==NULL) root = p;//first element in tree
    else if(x<father->data) father->leftchild = son;
    else father->righttchild = son;
}

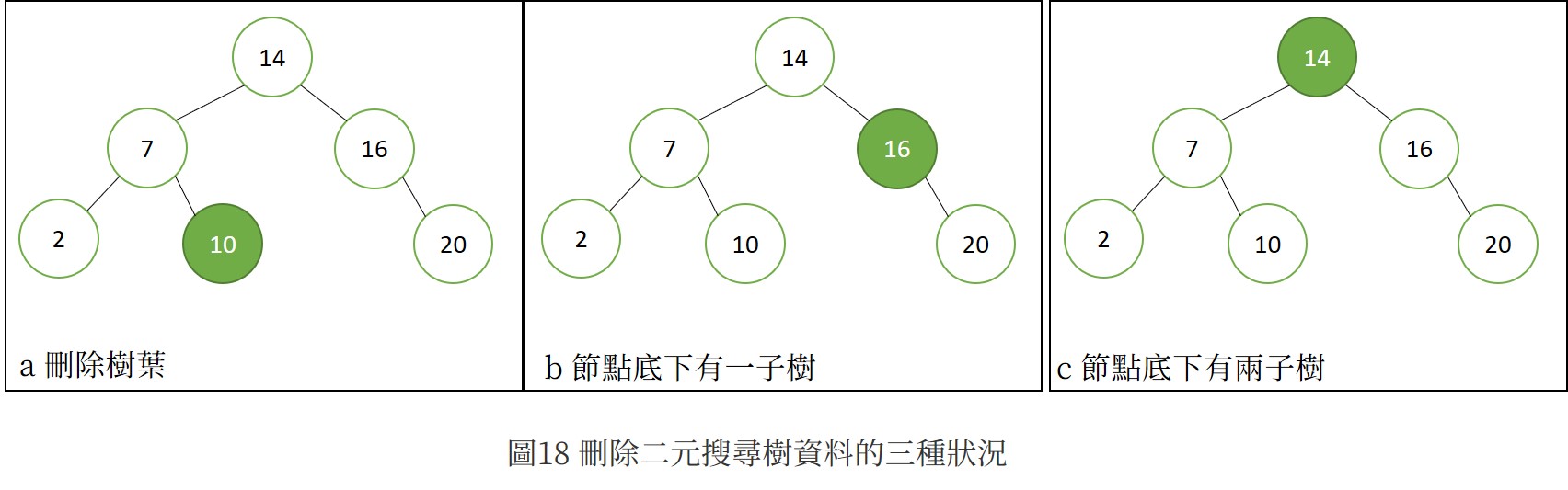
刪除資料

刪除二元搜尋樹上的資料時，會發現有三種情形(圖18)，以下將以遞迴及非遞迴的方式探討。

遞迴

1. (a)刪除樹葉

   直接將樹葉刪除，而其父節點因為遞迴的迴傳概念，也會接收到其子節點被改為NULL的情形。因此僅需下面步驟即可完成:

   //node為欲刪除節點
   temp = node;
   node = NULL;  //回傳時讓父節點知其Son為NULL
   free(temp);

2. (b)刪除有一子樹的節點

找到子樹的樹根取代即可。

//node為欲刪除節點
temp = (node->leftchild) ? node->leftchild:node->rightchild; //確認Node的右或左子樹哪個存在
*node = *temp;//取代被刪掉的位置
free(temp);

3. (c)刪除有兩子樹的節點

   以其右子樹中的最左樹葉(稱為「中序直接後繼元素(in-order successor)」)取代可維持正確性。

   struct BSTreeNode *InOrderSucc(struct BSTreeNode *node)
   {   struct BSTreeNode *p;
       for(p=node;p->leftchild!=NULL;p=p->leftchild);
       return p;
   }
   //delete
   temp = InOrderSucc(node->rightchild);//找到中序直接後繼元素
   node->data = temp->data;
   node->rightchild = DeleteBSTNode(node->rightchild,temp->data);

完整版

 struct BSTreeNode *InOrderSucc(struct BSTreeNode *node)
 {  struct BSTreeNode *p;
     for(p=node;p->leftchild!=NULL;p=p->leftchild);
     return p;
 }
 struct BSTreeNode *DeleteBSTNode(struct BSTreeNode *node,int x)
 {
     struct BSTreeNode *temp;
     if(node==NULL) return node;
     //search
     if(x<node->data) 
         node->leftchild = DeleteBSTree(node->leftchild,x);
     else if(x>node->data)
         node->rightchild = DeleteBSTree(node->rightchild,x);
     //x found in node
     else
     {  //sitaution a or b
         if((node->leftchild==NULL)||(node->rightchild==NULL))
         {
             temp = (node->leftchild)?node->leftchild:node->rightchild;
             if(temp==NULL)//a -> leaf
             {
                 temp = node;
                 node = NULL;
             }
             else *node = *temp; // b -> one subtre 
             free(temp);
         }
         else //c -> two subtree
         {
             temp = InOrderSucc(node->rightchild);//找到中序直接後繼元素
             node->data = temp->data;
             node->rightchild = DeleteBSTNode(node->rightchild,temp->data);
         }
     }
 }

Heap 堆積

Heap 是一種特殊的完備二元樹，節點與其子節點之間有定好的大小關係存在。分為以下兩種：

定義：

1. 最大堆積：為一完備二元樹，任一節點的資料內容不小於其子節點的資料內容。
2. 最小堆積：為一完備二元樹，任一節點的資料內容不大於其子節點的資料內容。

堆積因為其特性，發展出「堆積排序(Heap Sort)」及「優先佇列(Priority Queue)」等。以下運用陣列表示完備二元樹的方式來操作以下兩種動作，假設現在有一最大堆積，存放於陣列A[1]~A[n]中：

新增資料x

1. 為維持樹符合完備二元樹之定義（白話文：有缺一定在右下角），先將資料加在最後一節點註標之後（註標i=n+1），將x放在A[i]。
2. 再來為了維持「父節點必須大於子節點」之特性，逐一向上檢查i與父節點(i/2)的大小關係是否需要調換位置，直至檢查到最上面的兒子（root下一層）。

#define maxsize 100
int n,i;//n is number of elements in heap
int heap[maxsize];
void InsertHeap(int x)
{   if(n==maxsize) HeapFull();
    else
    {   n++;
        i=n;
        while((i>1)&&(x>heap[i/2]))
        {   heap[i]=heap[i/2];
            i/=2;
        }heap[i]=x;
    }
}

刪除資料x（x為堆積中最大值=root）

1. 取出root資料後，會剩下兩個最大堆積，將最後一節點n資料拿到root存放，此時畢定不符合最大堆積定義。
2. 從樹根出發，選取其子節點中較大者比較，若父節點大於子節點則終止；否，則交換，一直持續到找到樹葉節點為止。

//其餘設定承上面範例
int x,i,j;
int DeleteHeap()
{   
    if(n==0) HeapEmpty();
    else
    {   x = heap[1];
        heap[1]=heap[n];
        n--;
        i=1;
        while(i<=n/2)//持續尋找直到找到樹葉節點
        {
            if(heap[2*i]>heap[2*i+1]) j=2*i;
            else j=2*i+1;
            if(heap[j]<heap[i]) break;
            else
            {
                SWAP(&heap[j],&heap[i]);
                i=j;
            }
        }return x;
    }
}