Sorting排序

排序是重要且經常使用的運算。例如在資料整理搜尋排序時都有排序的需求；以二元搜尋法在排序過的資料進行搜尋是許多搜尋問題的核心技術；資料庫的設計也十分著重於資料的搜尋及排序。另外，許多組合問題（combinatorial problem）也都以排序作為其前置運算（pre-processing），例如在加權圖形中找最小延展樹的Kruskal演算法，就得先將所有的邊依距離排序。

排序的考量

資料存放位置

依據資料存放位置不同，可以分成兩種，在存取速度方面有顯著的差異。本文以內部排序為主。

內部排序法（internal sorting）：資料全部在主記憶體中。
外部排序法（external sorting）：主記憶體僅存放部分資料，大部分的資料皆在外部記憶體（如：硬碟、磁帶、檔案等）中。

主記憶體屬於隨機存取設備（random access device），速度較快。

外部記憶體則是循序存取設備（sequential access device），速度慢上許多，通常處理的資料量較大。

穩定性

指的是排序後的擁有相同值的資料是否可以維持原先的順序，若可則稱該演算法具有穩定性。

具穩定性的排序演算法執行結果範例（可以看到2和2*的相對位置並未改變）

排序前：12, 5 , 2, 6 ,9 , 2*
排序後：2, 2* ,5 ,6 ,9 , 12

排序演算法

範例皆以小到大排列。

Selection Sort
Insertion Sort
Bubble Sort
Merge Sort
Quick Sort
Heap Sort

Selection Sort 挑選排序法

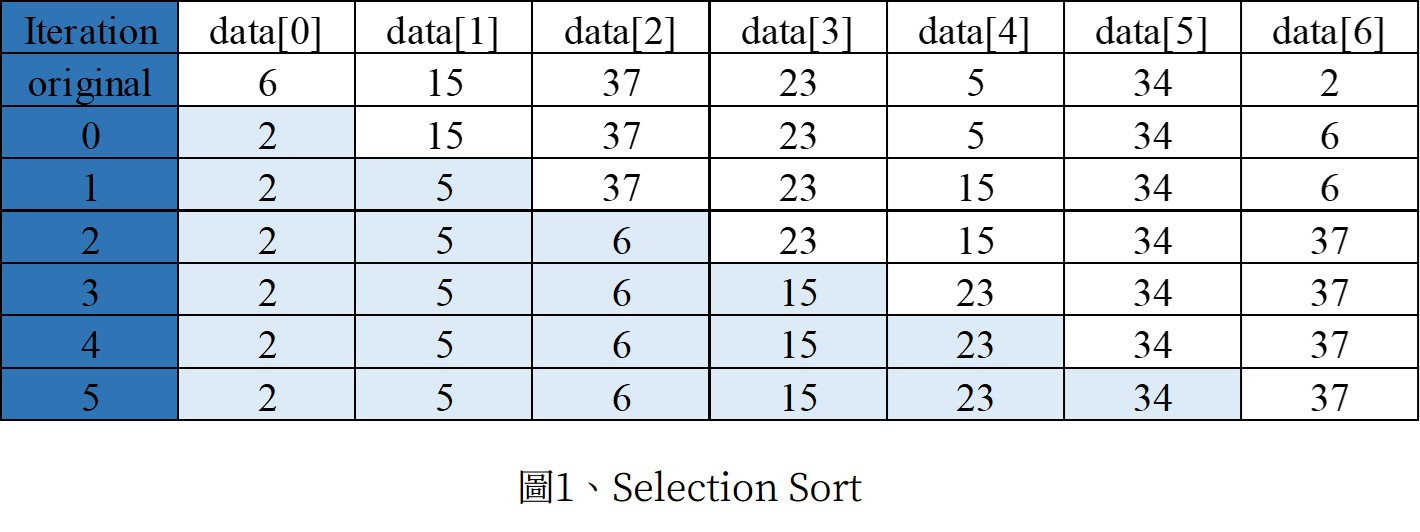
概念： 在產生排序陣列時，每次都挑選最小的放進來

自起始位置開始，逐一往其右進行比較，找到其右手邊最小之值後，與其交換。n筆資料共需執行n-1次比較，帶n-1都排序完後，第n筆資料自然也是正確的排序結果。

內部資料夾內

Input : 整數陣列data，長度為n
Output : 排序陣列data，若i<j，則data[i]≦data[j]，0≦i,j<n

void SWAP(int *x,int *y)
{
    int temp;
    temp = *x;
    *x = *y;
    *y = temp;
}
void SelectionSort(int data[],n)
{   int i,j,min;
    for(i=0;i<n-1;i++)
    {
        min = i;
        for(j=i+1;j<n;j++)
        {
            if(data[j]<data[min]) min = j;
        }
        SWAP(&data[i],&data[min]);
    }    
}

時間複雜度

Insertion Sort

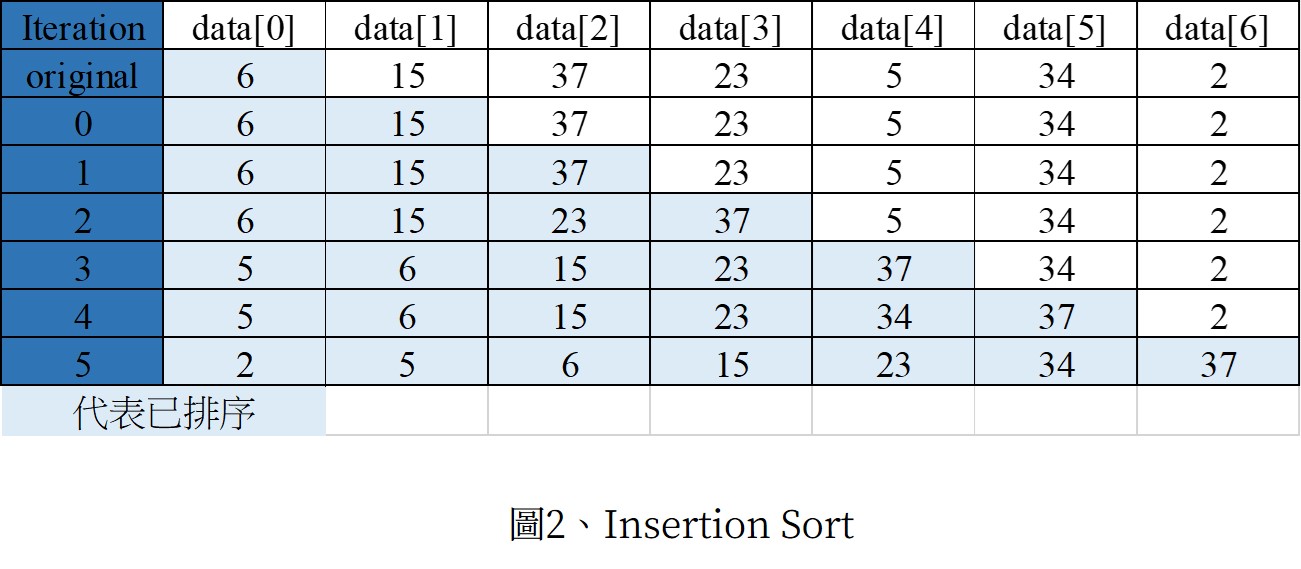
概念 : 每次將一個為排列的值加入已排序的陣列

第1個值是"已排序陣列"，因此會從第2個值開始一個一個加入已排序陣列中該值應該在的位置（符合大小順序）。

內部資料夾內

Input : 整數陣列data，長度為n
Output : 排序陣列data，若i<j，則data[i]≦data[j]，0≦i,j<n

void InsertionSort(int data[],n)
{   int i,j,target;
    for(i=1;i<n;i++)
    {
        target = data[i];
        j=i;
        while((j>0 )&& (data[j-1]>target))//調整已排序陣列，找到target該在的位置
        {
            data[j] = data[j-1];
            j--;
        }
        data[j] = target;
    }    
}

時間複雜度

Bubble Sort

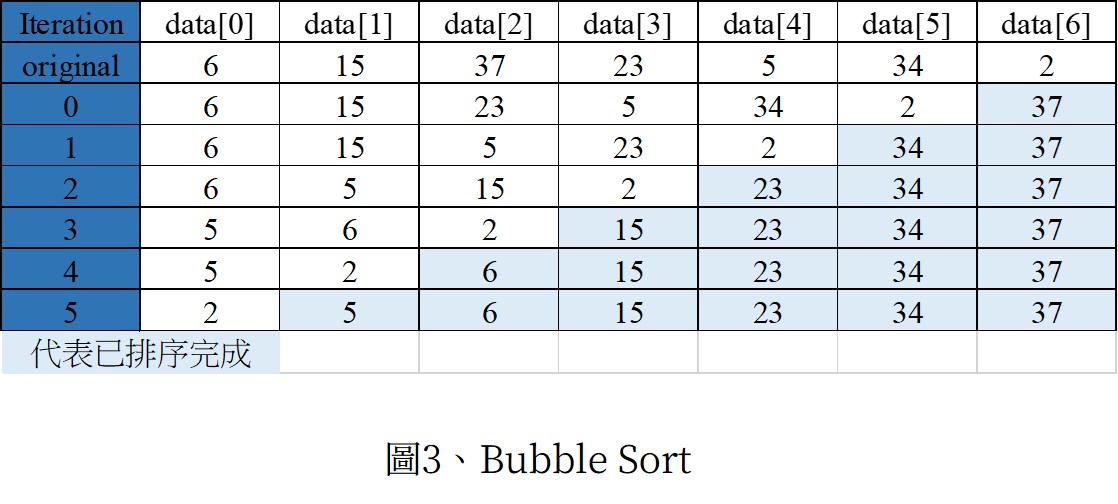
概念 : 大資料往下，小資料往上

藉由相鄰兩兩比較交換，每次迴圈都會找到未排序中最大的值，並且最終被放置到最底。

內部資料夾內

Input : 整數陣列data，長度為n
Output : 排序陣列data，若i<j，則data[i]≦data[j]，0≦i,j<n
void SWAP(int *x,int *y)
{
    int temp;
    temp = *x;
    *x = *y;
    *y = temp;
}

void BubbleSort(int data[],int n)
{   int i,j;
    for(i=n-1;i>1;i--)
        for(j=0;j<i;j++)
            if(data[j]>data[j+1]) SWAP(&data[j],&data[j+1]);
}

時間複雜度

Merge Sort

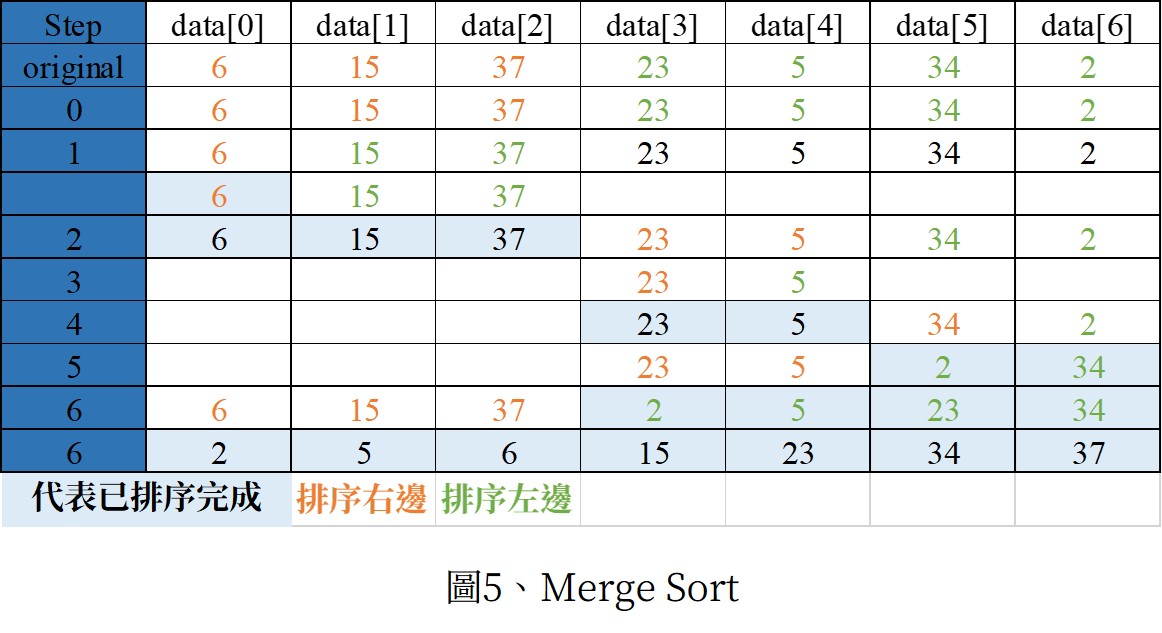
概念 : 將兩個已排序好的陣列合併

內部資料夾內

merge
共三個陣列，已排序之A、B陣列以及用來儲存最終陣列的C，依序從AB中拿出最小的互相比較，較小的就先放進C中。若AB其中一陣列已放完，代表另一陣列的值都較大，可將其直接併入C。
merge sort
將一陣列丟入該函式中，取其中間註標，排序註標左邊、排序註標右邊(遞迴概念)，當剩一個值的時候，該值就是一排序完成的陣列，可進行合併，如此一來再回傳，最終得以完成整個陣列的排序。

//1.merge
Input : 已排序整數陣列A，長度為m；已排序整數陣列B，長度為n
Output : 排序陣列C，若i<j，則C[i]≦C[j]，0≦i,j<m+n
void Merge(int C[],int k,int A,int i,int m,int B,int j,int n)// k,i,j為ABC的起始註標；m、n為AB的長度
{   int C1[n+1];//實作上的考量
    int k1=k;//實作上的考量
    int n1=n;//實作上的考量
    while((i<=m) && (j<=n))
    {
        if(A[i]<=B[j]) C[k++]=A[i++];
        else C[k++]=B[j++]
    }//end when A or B is all sorted
    while(i<=m) C[k++]=A[i++];//put all left A into C
    while(i<=m) C[k++]=B[j++];//put all left B into C
    for(int x=k1;x<n1+1;x++) C[x]=C1[x];//實作上的考量
}
//2.merge sort
Input : 整數陣列data，起始註標right、終點座標left
Output : 排序陣列data，若i<j，則data[i]≦data[j]，0≦i,j<n
void MergeSortRecur(int data[],int right,int left)
{   int m;
    if(left<right)
    {
        m = (left+right)/2;
        MergeSortRecur(data,left,m);
        MergeSortRecur(data,m+1,right);
        Merge(data,left,data,left,m,data,m+1,right);
    }
}
Input : 整數陣列data
Output : 排序陣列data，若i<j，則data[i]≦data[j]，0≦i,j<n
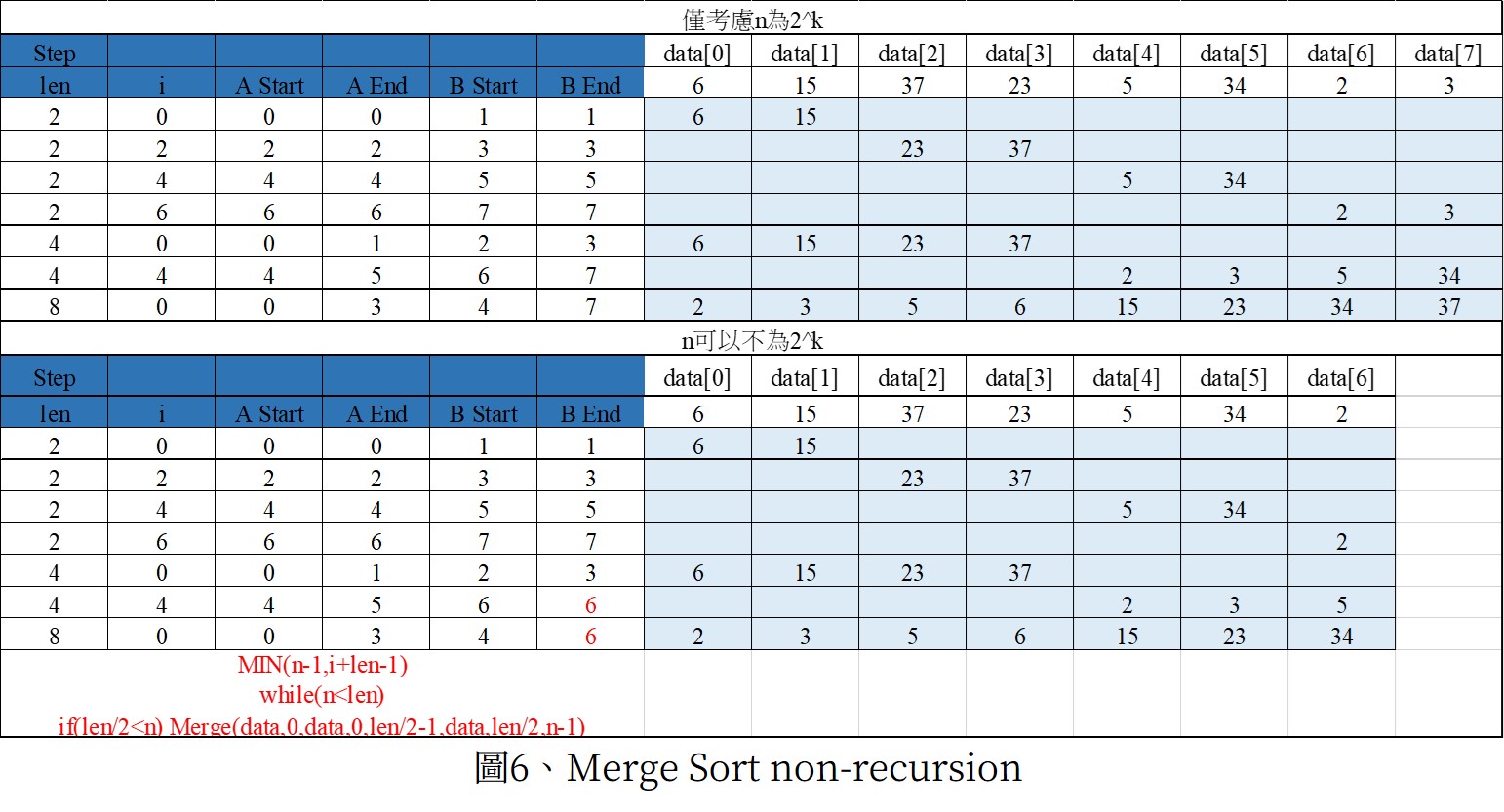
//僅考慮n為2^k
void MergeSort(int data[])
{   int len=2;
    while(len<=n)
    {   for(i=0;i<n;i+=len)
        {   Merge(data,i,data,i,i+len/2-1,data,i+len/2,i+len-1);
        }len*=2;
    }
}
//n可以不為2^k
void MergeSort(int *data)
{   int len=2;
    while(len<n)
    {   for(int i=0;i<n;i+=len)
        {   Merge(data,i,data,i,i+len/2-1,data,i+len/2,MIN(n-1,i+len-1));
        }len*=2;
    }
    if(len/2<n) Merge(data,0,data,0,len/2-1,data,len/2,n-1);
}

非遞迴版本的排序步驟:

內部資料夾內

Quick Sort

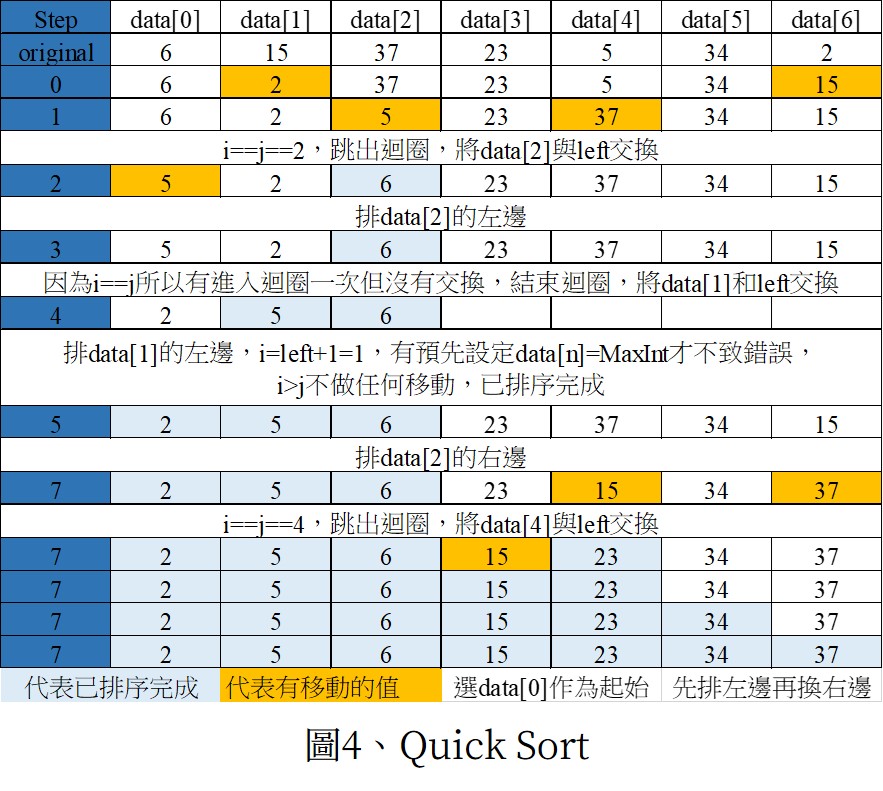
概念 : 每次將一個未排序值放去它該在的位置

從頭開始，將該值放去它在陣列中該在的位置，由於該位置左邊的值皆較小；而右邊的直接較大，代表接下來要排序可以用兩個一半的陣列去排，因為左右兩半必定不會有需要交換的情形。

如何將較小擺在target左邊、較大擺在taget右邊?

使用兩註標i , j，i自left處開始；j自right處開始。i持續往右移動，直到找到一值大於target；j持續往左移動，直到找到一值小於target，接者交換i、j的值。當i==j時代表已排序完，亦及該位置為target所該在的位置。

將data[n]的值設為MaxInt(系統所允許的最大整數)，以避免i的移動出錯

內部資料夾內

Input : 整數陣列data，起始註標right、終點座標left
Output : 排序陣列data，若i<j，則data[i]≦data[j]，0≦i,j<n
void SWAP(int *x,int *y)
{
    int temp;
    temp = *x;
    *x = *y;
    *y = temp;
}
void QuickSortRecur(int data[],int left,int right)
{   int i,j,target;
    if(left<right)
    {
        i = left+1;
        j = right;
        data[n] = MaxInt;//避免註標i++時會產生錯誤之特殊情況
        target = data[left];
        do
        {   while(i<=j && data[i]<target) i++;//找到比target大的註標位置
            while(j>=i && data[j]>target) j--;
            if(i<j) Swap(data[i],data[j]);
        }while(i<j)
        if(left<j) Swap(data[left],data[j]);//把target放到它該在的位置
        QuickSortRecur(data,left,j-1);
        QuickSortRecur(data,j+1,right);        
    }
}
void QuickSort(int data[],int left,int right)// Non-Recursion version
{   int i,j,target;
    push(left,right);
    while(stack is not empty)
    {
        (left,right) = pop();
        target = data[left];
        i = left+1;
        j = right;
        do
        {   while(i<=j && data[i]<target) i++;//找到比target大的註標位置
            while(j>=i && data[j]>target) j--;
            if(i<j) Swap(data[i],data[j]);
        }while(i<j)
        if(left<j) Swap(data[left],data[j]);//把target放到它該在的位置
        if(right>j+1) push(j+1,right); 
        if(left<j-1) push(left,j-1);        
    }
}

Radix Sort

概念 : 依序對每一位數進行排列

基數排序法和前面所用的排序概念不太一樣，其大小比較與輸入數列的基底位數有關。假設輸入數列皆為三位數，那麼先針對其百位數字相同進行排列，再將各序列依照十位數字相同排列，最後是個位數字相同進行排列，這種"由高到低位數"的排列稱為"高位數優先(most significant digit first)"；"低到高位數"則是"低位數優先(least significant digit first)"，可以得到相同結果。這裡以低位數優先來操作。

兩種優先方法在操作上的不同:

Least : 將欲排序序列依照低位數放入佇列，產生新的序列，再將其依照高位數排列。

Most : 將欲排序序列依照高位數放入佇列，針對每一佇列，將其依照低位數排列。

內部資料夾內

圖7可見，以十個佇列存放的方式來操作的概念是沒有問題的。然而，直接以此進行恐會浪費記憶體空間，因此以陣列的方式操作，畢竟我們要儲存的就是n個值，只需要大小為n的陣列。

以圖8為例，利用count數每個佇列裡有多少元素，再用index表示欲儲存該佇列時，起始註標應為多少。例如下圖中十位數為3的佇列應從註標index=5開始儲存。

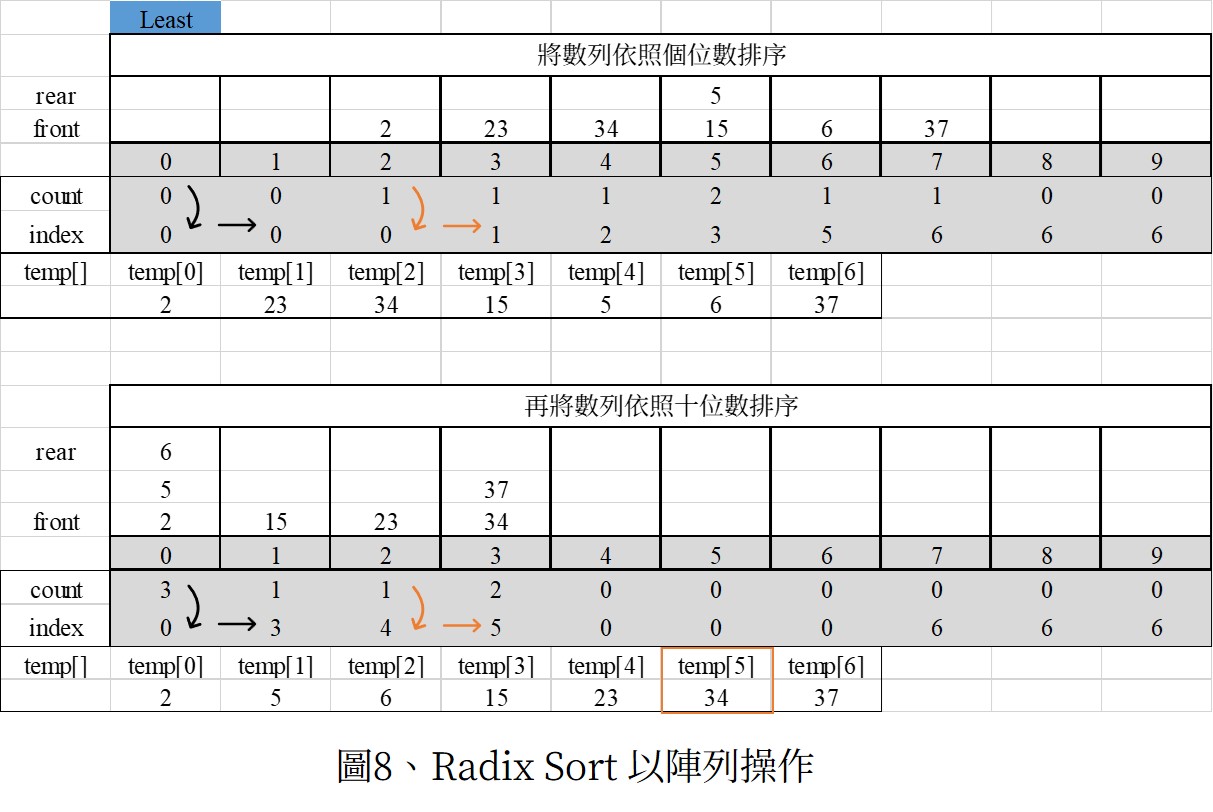
內部資料夾內

在此演算法中，其實並未使用到「比較大小」的指令，另外，使用了額外的陣列count[]及index[]來儲存必要資訊，資料量的搬移十分可觀。適用情況在於：資料的位數不太且相近（例如：身分證字號、學號、車牌等），也沒有記憶體空間的考量。

Input : 整數陣列data，共n筆資料
Output : 排序陣列data，若i<j，則data[i]≦data[j]，0≦i,j<n
int count[10];//store queue from 0~9
int index[10];//store start index of queue from 0~9
//取得最大值的位數
int max=0;
for(i=0;i<n;i++)
{
    if(max<data[i]) max = data[i];
}
int radix = ceil(log(max+1));
//從低位數開始排
for(i=1;i<=radix;i++)
{
    for(j=0;j<10;j++) count[j]=0;
    for(j=0;j<n;j++)
    {
        digit = data[j]的第i位數字;
        count[digit]++;
    }
    index[0]=0;
    for(j=1;j<10;j++) index[j]=index[j-1]+count[j-1];
    for(j=0;j<n;j++)
    {
        digit = data[j]的第i位數字;
        temp[index[digit]++] = data[j];
    }
    for(j=0;j<n;j++) data[j] = temp[j];
}

Heap Sort

在介紹樹的時候有介紹最大(小)堆積，在此以最小堆積來實作排序。

概念：不斷於最小堆積中取出最小值，並更新之

不斷取出並更新的做法其實就是之前在堆積實作過的刪除功能，以下以restore為包含「恢復失去樹根的兩最小堆積」功能的函式命名。

Input : 整數陣列data[s],data[s+1],...,data[t]，其中以data[2s]和data[2s+1]分別為樹根的左右子樹，且為最小堆積
Output : data[s],data[s+1],...,data[t]形成最小堆積
void restore(int s,int t)
{   int i,j;
    i=s;//設定為樹根
    while(i<=t/2)
    {
        if(data[2*i]<data[2*i+1]) j=2*i;
        else j=2*i+1;
        if(data[i]>data[j]) break;
        Swap(&data[i],&data[j]);
        i=j;     
    }
}

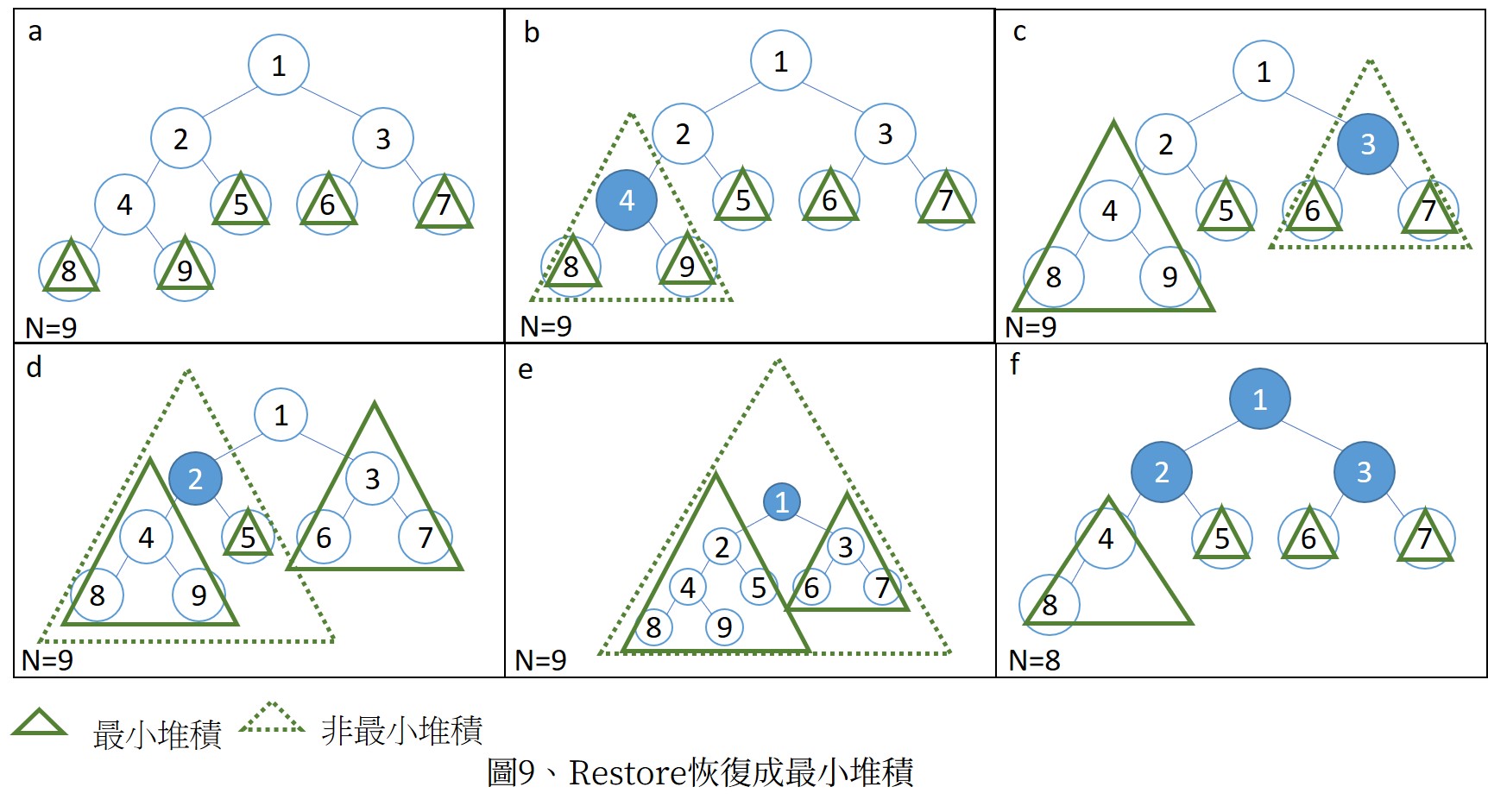
圖9(a)~(e)示範了利用restore建一最小堆積的步驟（奇數）以及(f)為偶數時的情況。

(a)~(e)中可看到樹葉節點本身就必定是最小堆積，因此就往樹葉節點的上一層去restore，也就是點4.3.2.1，以N值來表示就是for(i=n/2;i>=1;i--)的迴圈裡。

在(f)中可以發現點4.8已是一最小堆積（並非都是樹葉節點），因此只需要對點3.2.1作restore，以N值來表示就是for(i=(n-1)/2;i>=1;i--)`的迴圈裡。

可以發現使用for(i=(n-1)/2;i>=1;i--)的迴圈裡可以同時適用兩種情況!

內部資料夾內

for(i=(n-1)/2;i>=1;i--)
{
    restore(i,n);
}
for(i=n;i>=1;i--)
{
    output data[1];
    data[1]=data[i];
    restore(1,i);
}

Sorting排序

排序的考量​

資料存放位置​

穩定性​

排序演算法​

Selection Sort 挑選排序法​

Insertion Sort​

Bubble Sort​

Merge Sort​

Quick Sort​

Radix Sort​

Heap Sort​

排序的考量

資料存放位置

穩定性

排序演算法

Selection Sort 挑選排序法

Insertion Sort

Bubble Sort

Merge Sort

Quick Sort

Radix Sort

Heap Sort