Graph圖形
圖形是包含點和連接點的邊,所組成的離散結構。可用來描述許多實際問題。 圖形Graph是非常廣泛使用的資料結構,許多常見問題可用「點」(vertex)和「邊」(edge),描繪出對應的「圖形表示法」(graph representation)。如此一來,圖形理論(graph theory)上的許多性質可被用來解決所轉換的問題。
問題的圖形表示法
幾個著名且可用圖形描繪的問題。
尤拉迴路(Eulerian Circuit)
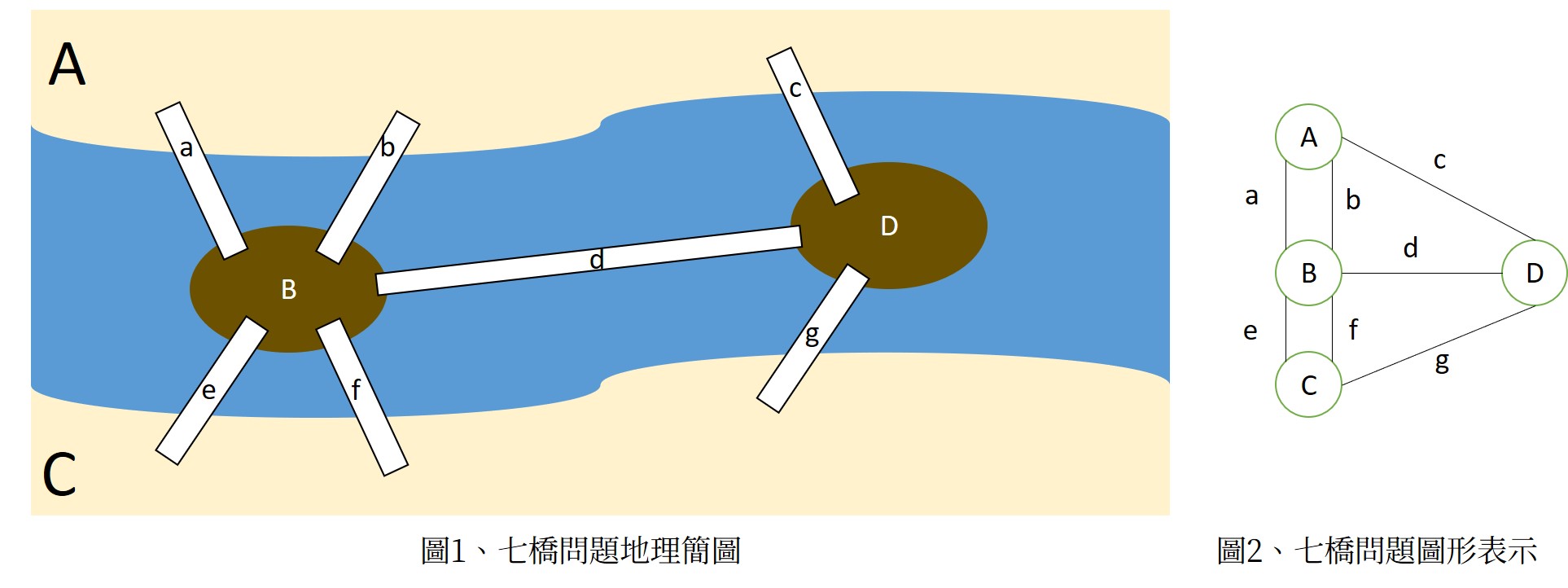
西元1763年,尤拉利用圖形來描繪東普魯是柯尼斯堡的「七橋問題」(圖1),圖中有ABCD四塊陸地及七座橋聯絡,七橋問題即盼望能走訪各城市僅經過所有橋一次。將圖1轉以圖形表示法即為圖2,同時定義原七橋問題欲尋覓的方法,「尤拉迴路(Euler tour(circuit))」: 自某頂點出發,走過所有邊恰好一次,最後回到出發點;「尤拉路徑(Eulerian path(walk))」: 則表示起點及終點不必相同。
尤拉證明 : 『相連圖形上存在尤拉迴路,若且唯若每一頂點的分支度(degree)皆為偶數』且『相連圖形上存在尤拉路徑,若且唯若且有兩個(或沒有)頂點分支度為奇數,其餘皆為偶數』。七橋問題不存在尤拉迴路及尤拉路徑,無解。此種轉換問題以點及邊表示的抽象技巧,奠定了圖論研究的基礎。
漢米爾頓迴圈(Hamiltonian Cycle)
漢米爾頓提出一個問題 : 在十二面體中,若每一頂點代表一城市,能否走過每一城市恰巧一次,且回到原出發城市(即此點會經過兩次)。此問題與尤拉迴路類似,差異在於尤拉迴路是希望走過每個「邊」一次(以迴路(Circuit)描述此類問題);此問題則是著重在「點」(以迴圈(Cycle)描述),且這類問題屬於NP-complete的問題。
旅行銷售員問題(Travel Salesman problem)
TSP問題希望能走訪每一個點一次,同時追求總成本(距離或時間等)要最小。求解此問題等同於在對應圖形上找到成本總和最小的漢米爾頓迴圈。
頂點覆蓋問題(Vertex Cover)
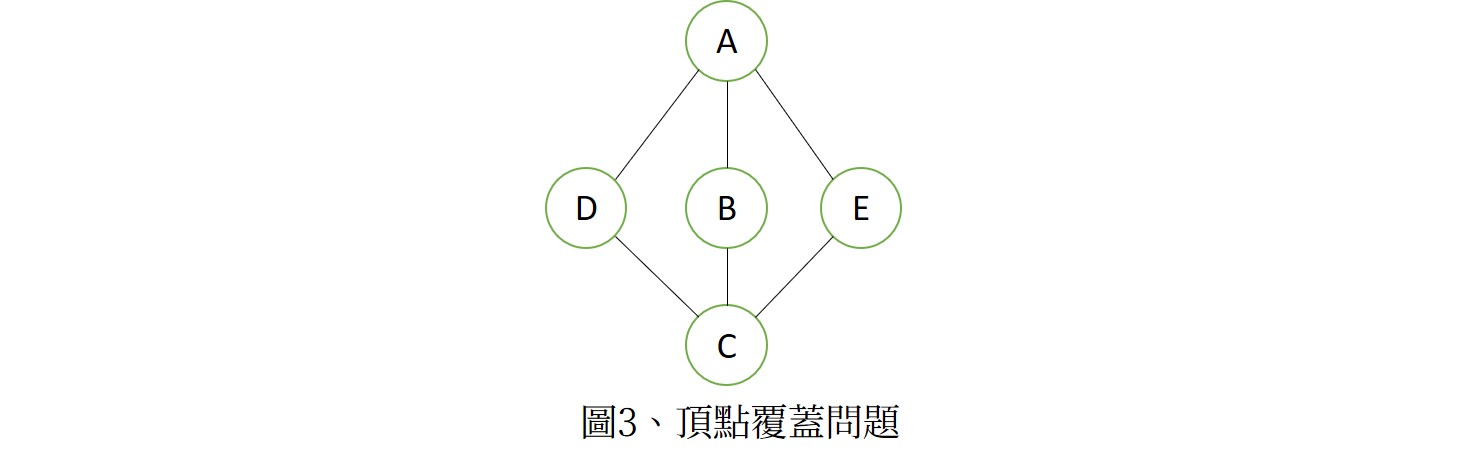
在博物館中有許多以兩頂點連成的邊作為走道,希望在最少的頂點處安裝監視器監視其所連接的走道(或公園內放置最少的燈,讓人至少可看到亮光)。轉換成圖形可如此描述:挑選最少的頂點,使得任何一邊的兩個頂點中,至少有一頂點在所挑的集合中。以圖3來說,AC及DBE是兩組可行的解,而AC這組姐所需較少頂點,且沒有更少個數的解,齊集唯頂點覆蓋問題的解。
專有名詞
常用G=(V,E)描述圖形,其中V是包含所有頂點的有限集合,E是連接V中頂點的邊所構成的集合;V={v1,v2,...,vn},E={e1,e2,...,em},n>0,m≧0。
無向圖、有向圖
無向圖(undirected graph)
e=(v1,v2),(v1,v2)和(v2,v1)代表相同的邊。
樹(Tree)是圖形的部分集合。
有向圖(directed graph)
e=(v1,v2),v1為頭(head);v2為尾(tail),(v1,v2)和(v2,v1)不是相同的邊。
在這裡討論的圖若無特別指明指的是無向圖,且討論的圖有下列限制:
圖形中任何頂點不允許有連接自己的邊,亦即沒有(v,v)、(u,u)的邊。
=> 無限制則稱為「自我迴圈(self-loop)」
圖形中的邊不得重複。
=> 無限制則稱為「多邊圖(multigraph)」

完備圖
在有n個頂點的無向圖中,至多有n(n-1)/2條邊。若該圖形確實有n(n-1)/2條邊,則稱為完備圖(Complete graph)。
而有向圖至多有n(n-1)條邊,若符合則稱為有向完備圖。
相鄰、連接、分支度
G = ( V , E )。
- 若(u,v) ∈ E ,則 u和v「相鄰」(adjacent);且(u,v)「連接」(incident on) u 和 v。
- 若G有方向性,而< u , v >∈ E ,則稱u「相鄰至」 (adjacent to) v;且v從u相鄰(adjacent from);< u , v >連接u、v。
- 所有連接在無向圖頂點u上的總邊數,稱為u的「分支度」(degree)。
- 在有向圖中,可分為out-degree及in-degree。
子圖
G = ( V , E ) 的子圖 G' = ( V' , E' )須滿足 V' ∈ V 且 E' ∈ E' 。
路徑、簡單路徑、長度、迴圈
- u到v的路徑(path)是由頂點u-v1-v2-...vi,v及其連接的邊(u,v1),(v1,v2),...,(vi,v)所構成(或<u,v1>,<v1,v2>,...,<vi,v>),以u-v1-v2-...-v表示此u到v的路徑。
- 簡單路徑(simple path)指的是除了起終點外,其他頂點皆不同的路徑。
- 迴圈(cycle)指的是起終點相同的簡單路徑。
- 圖5 ,A-B-C-D是一長度為3的簡單路徑
- 圖5 ,A-B-C-D-B是一長度為4的路徑,但不是簡單路徑
- 圖5 ,A-B-D-C-A 是一長度為4的迴圈

相連的頂點(或圖形)、相連組合
無向圖形G = ( V , E ) 。頂點u存在一路徑連接到頂點v,則稱頂點u和v是相連的(connected)。
無向圖形G的相連組合(connected component) C指的是圖中最大的相連子圖,亦即C是G的相連子圖中最大的。
強固相連、強固相連組合
有向圖形G = ( V , E ) 中,任兩點u、v,都存在兩條路徑 : 頂點u存在一路徑連接到頂點v,且頂點v存在一路徑連接到頂點u,則稱為強固相連(strongly connected)。強固相連組合(strongly connected component)為有向圖中最大且強固相連的子圖。
沒有迴圈
不存在迴圈的圖形稱為「沒有迴圈」(acyclic),一棵樹即為相連且沒有迴圈的圖形。由此可知圖 形graph是比樹tree更為一般化的資料結構,因此在對樹所做的動作運算皆可在圖形上探索。
圖形的資料表示
圖形是比樹更為一般化的資料結構,因此之前對樹所做的運算皆可在圖形執行。此介紹兩種常見的圖形資料結構「相鄰矩陣」、「相鄰串列」。
相鄰矩陣(adjacent matrix)
將頂點是否有相鄰的關係記錄在矩陣中。若G = ( V , E ),而|V|=n,即G有n個頂點。用一個n x n的二維矩陣A表示 : 令i,j ∈ V,若(i,j)∈E (或<i,j>∈E ),則Aij= 1,否則Aij=0。
根據上面敘述,可知相鄰矩陣是由0和1所組成。且無向圖形的相鄰矩陣是對稱的(即Aij=Aji);有向圖形則未必。另外,可計算其分支度:
無向圖形 : d(i) = ΣAij (j from 0~n-1)
有向圖形 : dout(i) = ΣAij (j from 0~n-1) 、din(i) = ΣAji (j from 0~n-1)
以矩陣解決圖形問題為O(n^2),若矩陣為稀疏矩陣(sparse),可以用相鄰串列表示。
相鄰串列(adjacent list)
G = ( V , E ),且|V|=n,G中的一頂點u的分支度為k,則可以將與u相鄰的k個頂點用鏈節串列串起,如此一來,n個頂點就會有n個鏈節串列。如圖6所示,以head指標指向每個頂點,每個頂點在各自串起有連結的頂點;其中,因為n個頂點是勢必不可省略的,因此用方便定址的陣列來宣告head,以方便用頂點編號作為陣列註標。

#define n 20
struct Node
{
int data;
struct Node *link;
};
struct Node *head[n];
若無向圖形有n個點,e條邊,則相鄰串列需要(n+2e)個儲存空間。
Q : 如何得知一給定圖形有多少條邊呢?
A1:以相鄰矩陣儲存,則查看有多少1,為O(n^2)
A2:以相鄰串列儲存,則走訪所有節點,為O(n+2e)
效率和圖形的疏密程度有關
對有向圖形而言,要得知向外分支度時,只需走訪該頂點串列,為O(n+e)。然而要計算向內分支度時,以圖6的形式則較不直覺,因此可再設計反向相鄰串列(inverse adjacent list)來表示,如圖7。

SSAD - Single source / All destination
單一起點至所有目的地的最短路徑:給予一有向圖形,圖中的邊都是非負的成本,尋找最短路徑。
Dijkstra 演算法
Input : weighted graph G = (V,E), V={0,1,2,...,n-1},
edge cost w[i,j], i,j∈V , origin u
Output : the shortest path from u to v
//初始化u到所有目的地v
for (v=0;v<n;v++)
{
D[v] = w[u,v]; //D[v] : u到v目前最短距離
C[v] = u; //u到v的最短距離是經由u提供
}
found[u] = true; D[u] = 0;//u到u的最短距離已被找到,其距離為0
while (還有目的地的最短距離未被找到)
{
k = min{v|D[v]為最小且found[v]為false};
found[k]=true; //u到k的最短距離已被決定
for(v=0;v<n;v++)
{
if(!found[v] && D[k]+w[k][v]<D[v])
{
D[v] = D[k]+w[k][v];
C[v] = k; //u到v的最短路徑包含(k,v)
}
}
}
output the shortest path from u to v //D[v],v∈V,u≠v//利用C[v]追朔u-v的最短路徑
印出 u-v的最短路徑
String ShortestPath(int u,int v)
{
String path = IntToStr(v);
while(C[v]!=u)
{
path = IntToStr(C[v])+"--["+IntToStr(w[C[v]][v])+"]"+"-->"+path;
v = C[v];
}
return path;
}
All Pairs
概念:每次加入一個點,如果他對任何兩點間的距離有幫助就加入。
Input : Graph G=(V,E),V={0,1,2,..n-1}和其相鄰矩陣w[i][j],0≦i,j<n。
Output : 任兩點間的最短距離矩陣A
for(int i=0;i<0;i++)
for(int j=0;j<0;j++)
A[i][j]=w[i][j];
for (int k=0;k<n;k++)
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
if(A[i][j]<A[i][k]+A[k][j])
A[i][j]=A[i][j]<A[i][k]+A[k][j]?A[i][j]:A[i][k]+A[k][j]
Search
DFS深先搜尋
遞迴
Input:Graph G=(V,E),V={0,1,2,..n-1}
Output:G的深先搜尋順序
int visited[n];
void DFS(int u)
{
visited[u]=1;
print u;
for(所有與u相鄰的頂點v)
{
if(v未曾走訪,即visited[v]!=1) DFS(v);
}
}
main()
{
for(int i=0;i<n;i++) visited[i]=0;
DFS(0);
}
堆疊
Input:Graph G=(V,E),V={0,1,2,..n-1}
Output:G的深先搜尋順序
int visited[n];
void DFS(int u)
{ push(u);
while(stack is not empty)
{ v=pop();
print v;
visited[v]=1;
for(w為v尚未走訪的相鄰頂點,即visited[w]!=1)
{
push(w);
}
}
}
BFS廣先搜尋
Input:Graph G=(V,E),V={0,1,2,..n-1}
Output:G的廣先搜尋順序
int visited[n];
main()
{
for(int i=0;i<n;i++) visited[i]=0;
visited[0]=1;
AddQ(0);
while(Q仍有頂點資料)
{
int u = Delete_Q;
print u;
for(所有與u相鄰的頂點v)
{
if(v未曾走訪,即visited[v]!=1)
{
visited[v] = 1;
AddQ(v);
}
}
}
}